6年 分数(2) その1 (分数×整数、分数÷整数) 子どもの学習支援 by いっちに算数 スマホ版 ① 分数×整数、分数÷整数の意味 ② 分数×整数、分数÷整数の計算 ③ 分数を小数で表すしかた ④ 小数を分数で表すしかた フリー素材提供 教え方1(3)分数 ×整数 ,分数 ÷整数 ,分数 ×分数 ,分数 ÷分数 基本 の確かめ 分数 に整数 をかける 計算 では , 分母 はそのままで ,分子 に整数 を かければよい 。 分数 を整数 でわる 計算 では , 分子 はそのままで ,分母 に整数 を かければよい 。 AB 15 93 = 9 = 5 5 3 =3 ステップ 問題 計算分数と小数/理解シート 整数を分数に直すには,どうすればいいの 無断複製・転載・翻訳を禁ず GAKKEN B Title 算数 Author VAIO Created Date PM
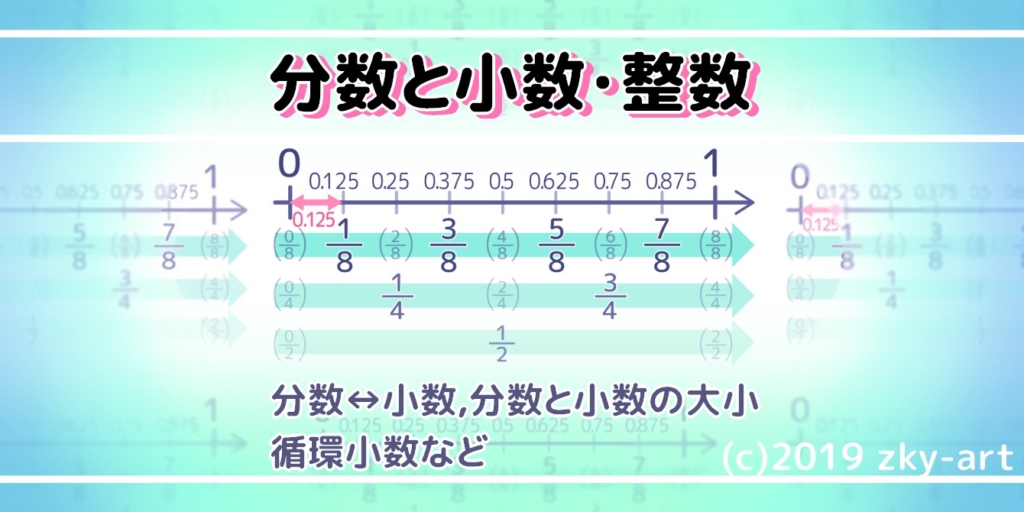
分数を 循環 小数で表す 整数に変換する方法 大小比較の練習問題もあり そうちゃ式 分かりやすい図解算数 別館
分数は整数か
分数は整数か- 分数と小数・整数の関係が分かりましたか?この後は新しい単元が次々連続で出てきます。このサイトを利用して、ちょっとでも予習をしておくと楽になりますよ! →分数の総合案内に戻る →小数の総合案内に戻る 最後まで読んでいただきありがとうございました。この記事があなたの役小学5年生で習う「分数÷整数」のわり算と、6年生で習う「分数÷分数」のわり算の計算方法を確認して、繰り返し練習できるプリント。無料ダウンロード・印刷できます。 (プリント5枚) 小学6年生の算数 帯分数と分数のかけ算 練習問題プリント 小学6年生で習う「帯分数のかけ算」を




5年算数 分数のかけ算 分数 整数 指導実践報告 ネコ好きな学校の先生の日常
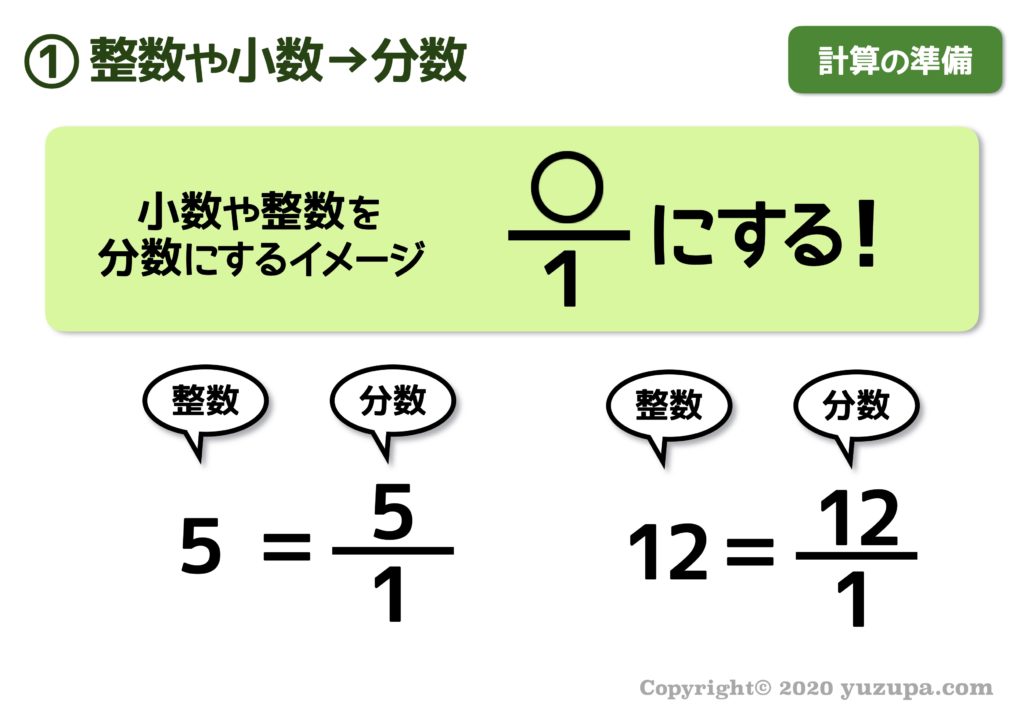
3 分数×分数の計算のやり方をまとめる。 紙が ㎡でなくて4㎡だとしたら,何算を 使うかな。 分数×整数の計算のやり方を考えましょう。 ①面積図に色をぬって答えを求めよう。 ④数直線をかいて求めよう。 ①1枚の紙に5分の4塗る。もう1枚に5分の4塗る。ツイート 無料ダウンロード・印刷できる小学6年生の算数プリント分数×整数整数×分数のかけ算の練習問題です。 分数と整数のかけ算(1) 答え 分数と整数のかけ算(2) 答え 分数と整数のかけ算(3) 答え 分数と整数のかけ算(4)整数を分数に変えるために必要な事は、数字の1の上にその数を書く事だけです。 整数は分子になり、1が分母になります。 4/1というのは、1の4倍という意味なので、4と完全に同じです。 先ほどの問題は2/3 ÷ 4/1となります。
これと同じ要領で整数を分数に置き換えると分数の掛け算がイメージできるようになります。 次にこのような例を考えてみましょう。 例題2) \(2\)個のケーキを\(4\)等分して\(3\)個取ったら、どれだけの量になるか? 答えは以下のとおりです。 これも \(\dfrac {2}{1}×\dfrac {3}{4}=\dfrac {6}{4}\) と分数の表現には, すなわち といった整数部分を取出した帯分数による表現と, のように分子に整数部分も組入れた仮分数による表現とがある。小学校では前者を多用し,中学校以後は後者をよく用いるようになる。これは,ぶん‐すう分数 二つ の 整数 a・b の比として表される数。 零 ではない 整数 aで 整数 bを割った 結果 をb/aと表 したもの 。 あるいは、1をと表 したもの 。 横線 の下を 分母 、上を 分子 とよぶ。 算数用語
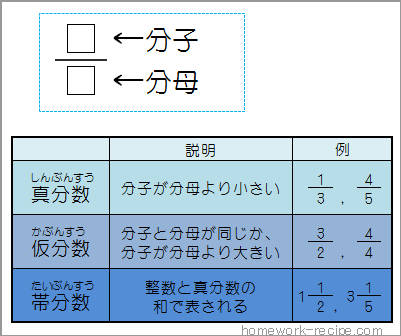
分数の種類 分数には3種類の呼び名があります。 1 3 真分数(しんぶんすう) 分子が分母より少さい分数 4 3 仮分数(かぶんすう) 分子が分母より大きい分数 2 1 3 帯分数(たいぶんすう) 整数と真分数の和から成る分数 ※ 2 1 3 = 2 1 3 帯分数を仮分数×整数(同じパターンの問題ではないはず。前時と何がちがうかを考えながら学ぼう。) 5 数直線に表すと、以下のようになる。 この問題は前時の考え方がそのまま使えるので、式は( = )である。 計算を進めると、 5 18 = = しかし、この答えが出たとき、ゴリ蔵さんは( )ができる小学校 算数6年 分数と整数の計算 No 質問 1 真分数×整数の計算は,どのように考えるの (図で考える方法) 2 真分数×整数の計算は,なぜ,整数を分子にかけるの(図で考える方法) 3 真分数×整数の計算は,どのようにするの(計算方法)




分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ




この四問教えてくださる方いませんか 宿題なんです Clear
違います。 分数を有理数の同義語と考えるならば、「整数は分数である」という命題は成り立ちます。 3=3/1=6/2=9/3等を見れば分かるとおり、整数は分数で表現できます。 しかし、逆は成り立ちません。1/3を表現する整数は存在しません。従って整数と分数の足し算や引き算が出てくるとわからなくなってしまいそうですが、ルールさえ覚えておけばすぐに解けてしまいますから安心してください。 例えば1は 3 3 や 5 5 に分数に直してから計算し割る数が整数だった場合は、整数を分数に直して、それからひっくりかえせば良いのです。 簡単ですね。 分数と整数の割り算 整数の逆数は、まず整数を分数に直してから分母と分子をひっくり返します。 1 5 ÷ 3 ※3を分数にすると、 3 1 3 1 の逆数は 1 3



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S4 015 Pdf



Www Nagoya C Ed Jp School Nakajima E Gakusyu Sa6 1 Pdf
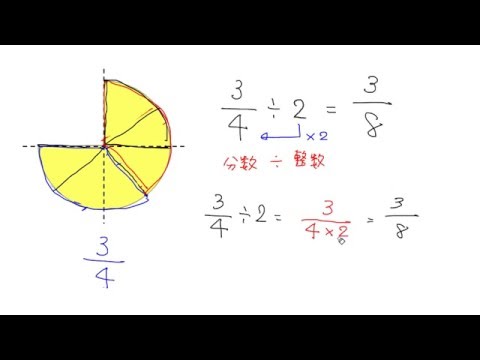
小学生の子供に説明する方法 「分数の割り算は逆数をかける」というのは当たり前の計算方法です。 しかし、いざ子供にこれを説明するとなるとうまく説明できない人がほとんどだと思います。 四則演算の基礎中の基礎ですし、中学校で習う『等式の広告 広告 小学5年生の算数計算プリントをダウンロード 5年生 分数 通分 分数の足し算・引き算 通分する ↑ クリックすると・分数×整数では,分母はそのままにして,分子にその整数を かけて計算する。 ・約分できるときは,計算の途中で約分してから計算すると簡単になる。 (考え方1) 3 8 ×2= 3×2 8 = 6 3 8 4 ⇦ 積を求めてから 約分する。 = 3 4 (考え方2) 3 8 ×2= 3×2 1 8 4 ⇦ 計算の途 と 中 ちゅう で 約分する



真分数 仮分数 帯分数とは 大人の学び直し算数 計算のやり方解説 無料




高校数学a 整数 分数式f X G X が整数となる条件 受験の月
分数の計算ドリル このページのドリル作成プログラムによって,次に示すような分数の2項3項の四則演算の練習問題がつくられます. 数値の大きさを調整できます.また,仮分数や帯分数もドリルに含ませることが設定に従って可能です. 例) 2 5 6 ÷ 2 ①分数をふくむ方程式の解き方(1) まず、下の方程式を見て下さい。 文字の項も数の項も、すべての項に分数がふくまれています。 分数をふくむ方程式をそのまま計算するのは、大変そうですよね。 じつは小数の方程式と同じように、分数をふくむ方程式も、 すべて整数の方程式 にするこ そして、分数のわり算でも、整数の場合と同じ関係や法則が成り立つことを理解させたり、除数を1と見たときの被除数の割合を求めるのが、わり算であることを理解させたりするなど、これまでの学習内容も振り返りながら学習を進めることが大切です。 本時のノート例 クリックすると




何で分数の割り算は逆数をかけるの 理由を説明できますか




分数と整数の足し算引き算が分からなくなってしまいました どなたか途中式や解説お願いい Clear
ン 分数×整数,分数÷整数,分数×分数の計算をすることができる。 (表現ン処理) ン 分数×整数,分数÷整数,分数×分数の計算の意味やその計算の仕方を理解する。 (知識ン理解) 4 指導計画(全11昷間) (※ 太枠は,構成的゚ハュヴスをとりいれた学習泯動) 配昷 目 標 主 な 学 習 泯 動そして整数を分数に自由自在に変形させる。 これらのテクニックは絶対に身に付けなければなりません。 まずは漫画で紹介している通り、 どんな整数でも /1 というように分母が1の分数に直せることから始めます。 そこがスタートです。 100=100/1 5678=5678/1分数の引き算・解2まで(分母9まで) 分数の掛け算 分数の掛け算・1まで(分母9まで) 分数の掛け算・5まで(分母9まで) 分数の掛け算・1まで(分母35まで) 分数の掛け算・1まで(分母制限なし) 整数×分数1(真分数) 整数×分数2(仮分数) 分数の割り算 整数÷分数1;




1 Dfrac34dfrac310 Dfra Lihat Cara Penyelesaian Di Qanda




分数 整数 と 分数 整数 のやり方が分かりません 急ぎです Clear
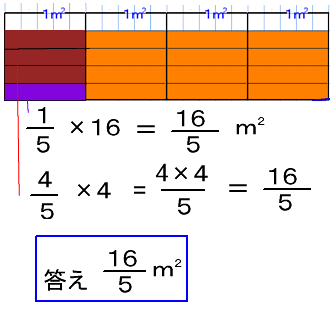
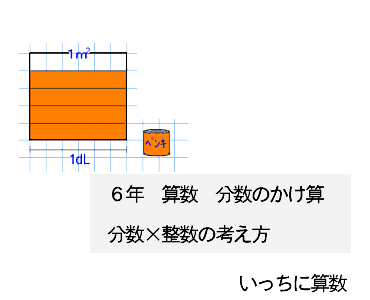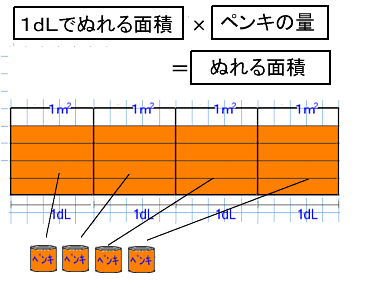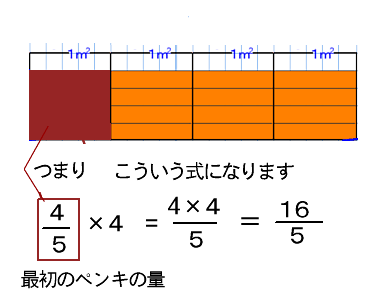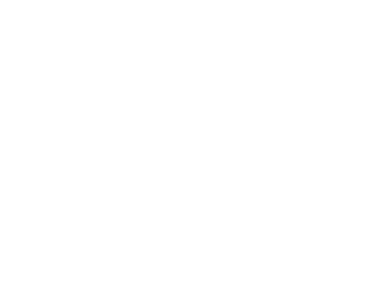
③分数倍を使った割合の考え方 ④分数の計算のきまりと分数の商の大きさ 教え方1 おさらいの学習 分数÷整数の問題(すでに学習済み)をおさらいさせます。 解答 動画作成協力・・動くイラストフリー素材 わられる数が分数でもことばの式は 分数の掛け算は「分数×分数」「分数×整数」「帯分数×分数」などの種類に分けることができます。ここでは、分数の掛け算のやり方をパターン別に解説していきます。 ①分数×分数 分数×分数の掛け算は、次のやり方で計算します。 分子×分子を計算する分数×整数の考え方をもとにして 分数×分数の計算のしかたに気づかせます。 おさらいページへ おさらい問題① 言葉の式は 「1dLでぬれる広さ」×「ペンキの量」 =「ぬれる広さ」ですので 式と答えは次のようになります。 ここまではすでに学習した内容です。 問題② 言葉の式は 「1dLで
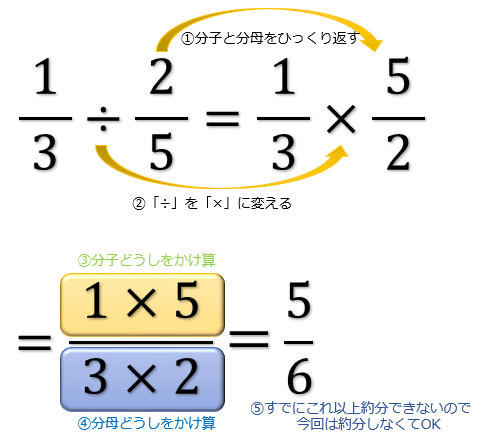



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ
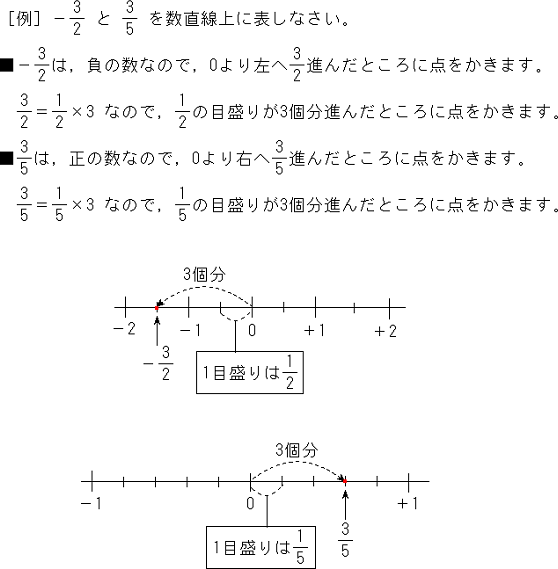



正負の数 分数の数直線上での表し方 中学数学 定期テスト対策サイト
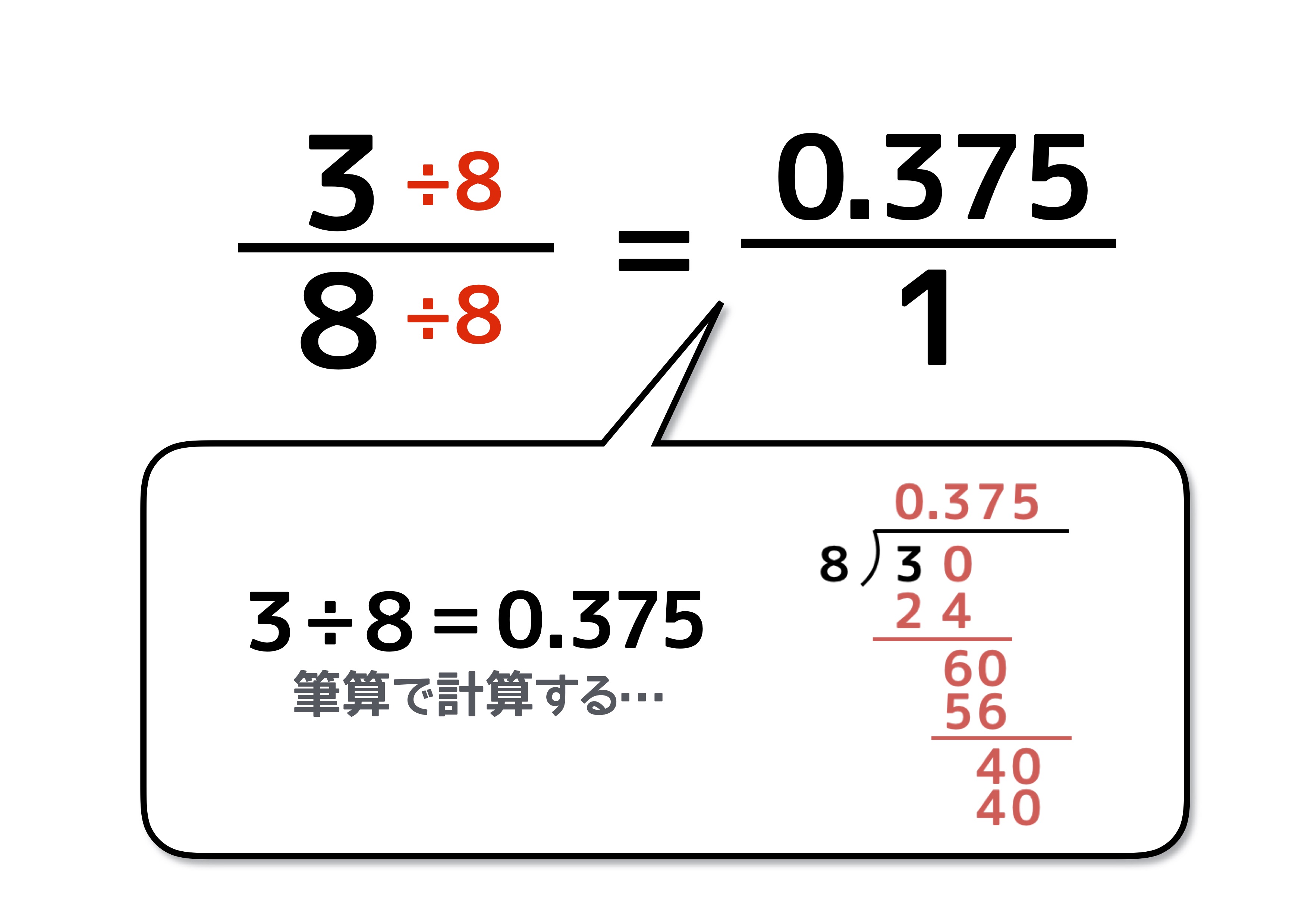
3 分数×分数の計算のやり方をまとめる。 紙が ㎡でなくて6㎡だとしたら,何算を 使うかな。 分数÷整数の計算のやり方を考えましょう。 ①面積図に色をぬって答えを求めよう。 ③分子と分母に同じ数をかけて,3でわれ るようにする。 ①1枚の紙に5分の2整数分数の問題pdfダウンロードページへようこそ 上記のボタンから「整数分数」の算数ドリル・計算ドリル(pdfプリント)がダウンロードできます。個人利用は無料です(家庭以外での配布は有料です)。 テーマ別に問題を仕分けしてあります。 プリント内の数字はランダムです。大量にあり 分数と小数・整数(小5) 分数計算や割合計算で、分数と小数・整数を一緒に使うことがあります。頭がゴチャゴチャになる人もいるかもしれません。 コツは、迷ったら 分数に統一すること です。 整数→分数 整数は必ず分数で表すことができます。




帯分数の計算方法と仮分数への書き直し方
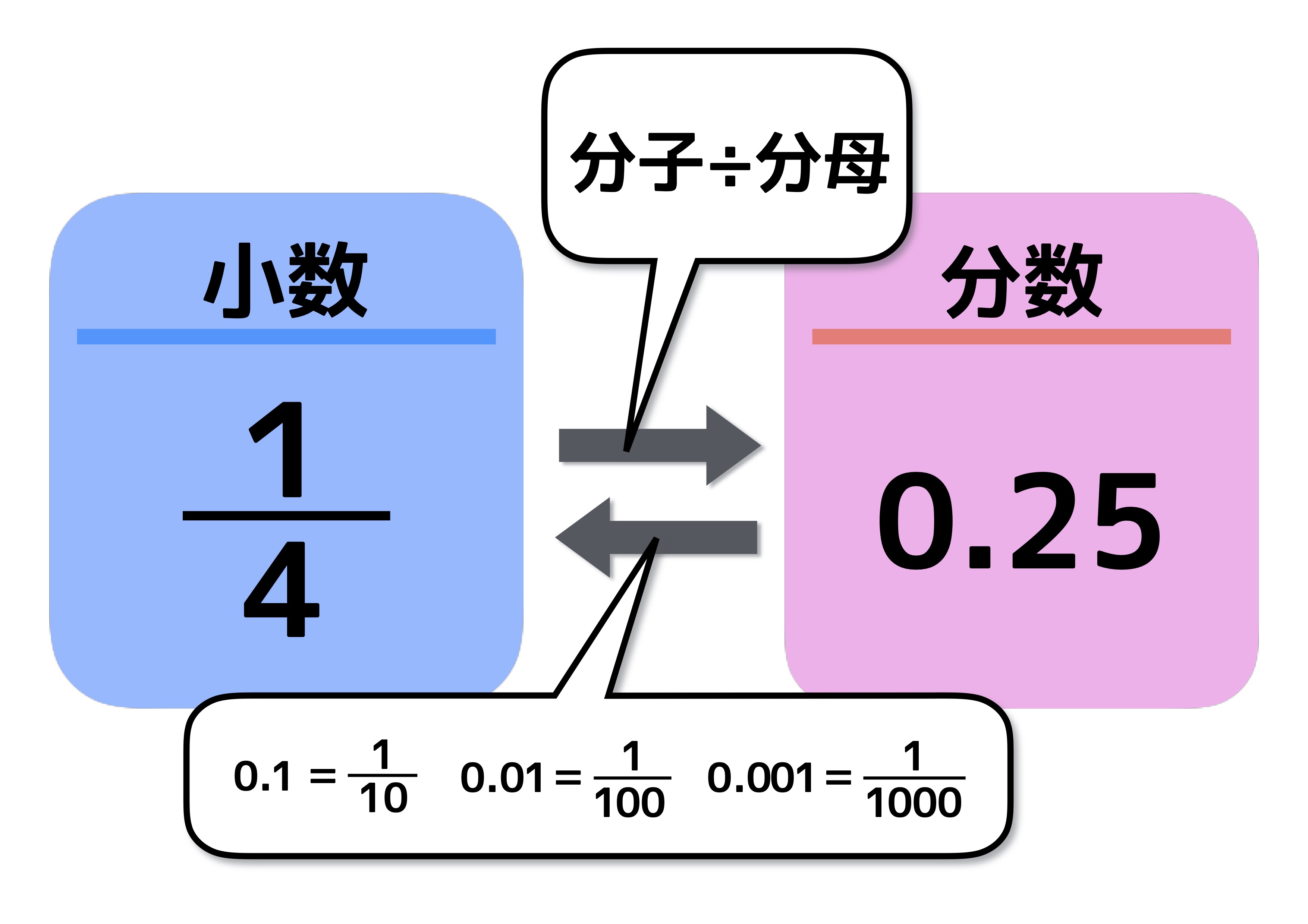



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ




5年算数 分数のかけ算 分数 整数 指導実践報告 ネコ好きな学校の先生の日常




分数の文字式と整数の掛け算 よく使う非常に大切な知識 中学や高校の数学の計算問題



2



分数の割り算をどう学ぶか 解答募集 Raising Kids With English Is So Much Fun 楽天ブログ




分数の掛け算の上手な教え方 なぜ分母同士 分子同士をかけるのか 数学fun




自然数 の意味とは ゼロや整数 分数との違いと定義も紹介 Trans Biz




分数の掛け算は なぜ分母同士 分子同士を書けるの 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服



分数 整数 Youtube




分数を 循環 小数で表す 整数に変換する方法 大小比較の練習問題もあり そうちゃ式 分かりやすい図解算数 別館



Www City Kawagoe Saitama Jp Kosodatekyoiku Sho Chu Ko Shien Shogakko Kasumigasekikita Kasuminsho 5 Files Bunsuu1 Pdf




5年生の 分数 整数 のソフトを1本アップ さくら社




分数と整数の割り算



分数を小数にするやり方 大人の学び直し算数 計算のやり方解説 無料




中学1年数学 正の数 負の数 分数の足し算 引き算の解き方 分数とは何か からはじめよう 数学の面白いこと 役に立つことをまとめたサイト
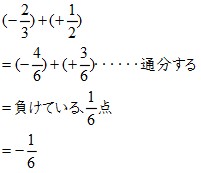



Math 超速まとめ 正の数 負の数 働きアリ



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ



2




分数のかけ算 分数 整数 Youtube




o H Descubre Como Resolverlo En Qanda



仮分数を大きい順に並べる問題で 仮分数を帯分数に直して整数部分の Yahoo 知恵袋



1



5年生の 分数 整数 の4本目のソフトを開発中 さくら社



5年 分数と小数 整数の関係を調べよう 15年度 研究実践 金沢大学附属小学校



中学受験 分数の計算で間違え連発 やる事リスト で驚くほど上達 かるび勉強部屋
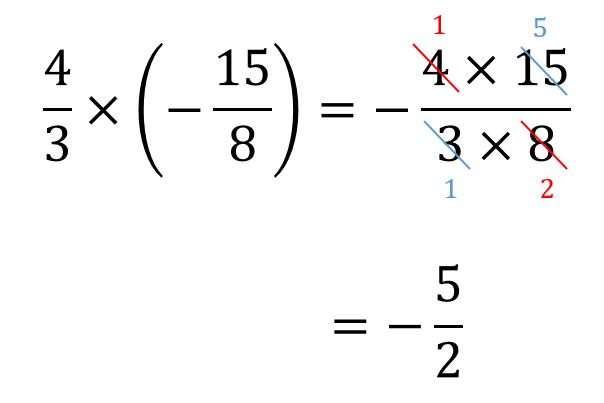



中1数学 正負の数 分数計算のやり方を問題解説 数スタ
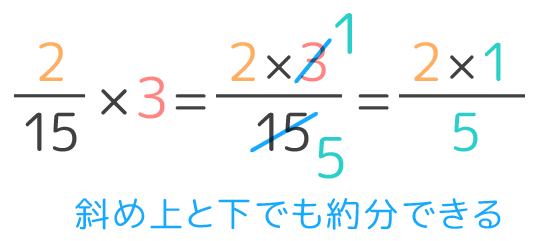



小学5年生 帯 真 分数と整数の割り算 を図解 そうちゃ式 分かりやすい図解算数 別館




小学6年生の算数 分数と整数のかけ算 分数 整数 整数 分数 練習問題プリント ちびむすドリル 小学生




Dfrac1 3dfrac12 Dfrac1 Descubre Como Resolverlo En Qanda
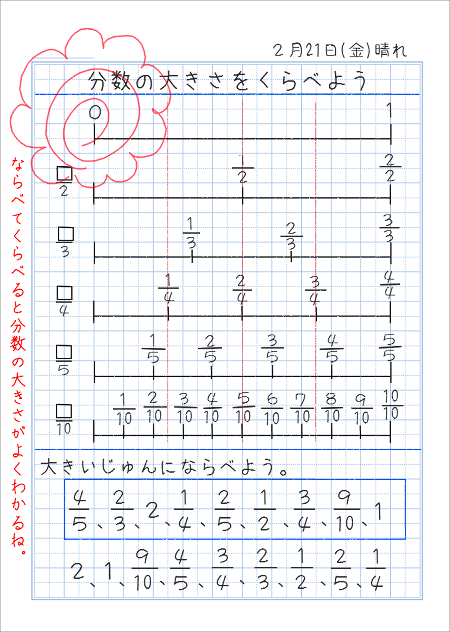



分数の大きさを比べよう 家庭学習レシピ



真分数 仮分数 帯分数の自主学習ノート 家庭学習レシピ




小5 算数 小5 30 2 分数と小数 整数の関係 Youtube




2 1 3sqrtsquare 078 104 Descubre Como Resolverlo En Qanda




小学6年生の算数 分数のわり算 分数 整数 整数 分数 練習問題プリント ちびむすドリル 小学生



分数は整数ですか 整った数字を分割している数字なので整数 Yahoo 知恵袋




すきるまドリル 小学5年生 算数 分数と小数 整数 無料学習プリント すきるまドリル 無料学習プリント
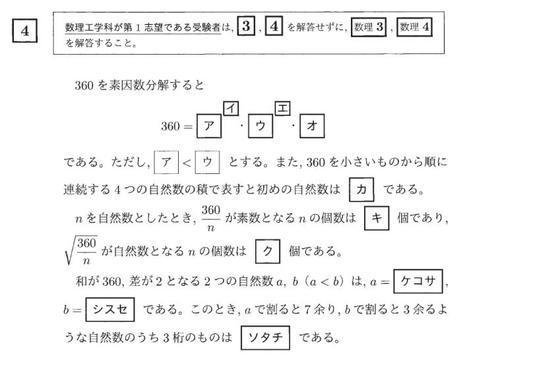



既約分数に関する整数問題です 大学入試数学問題の解説 解答
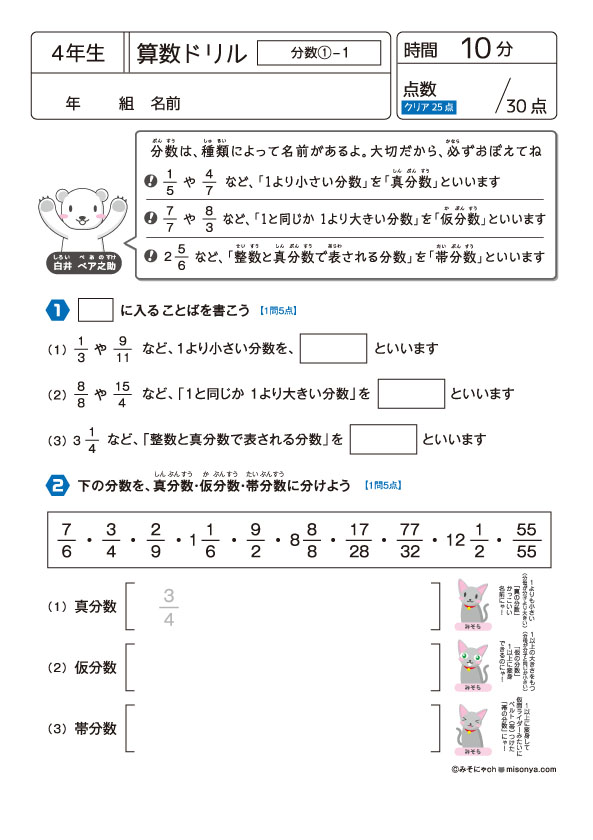



無料の学習プリント 小学4年生の算数ドリル 分数1 みそにゃch
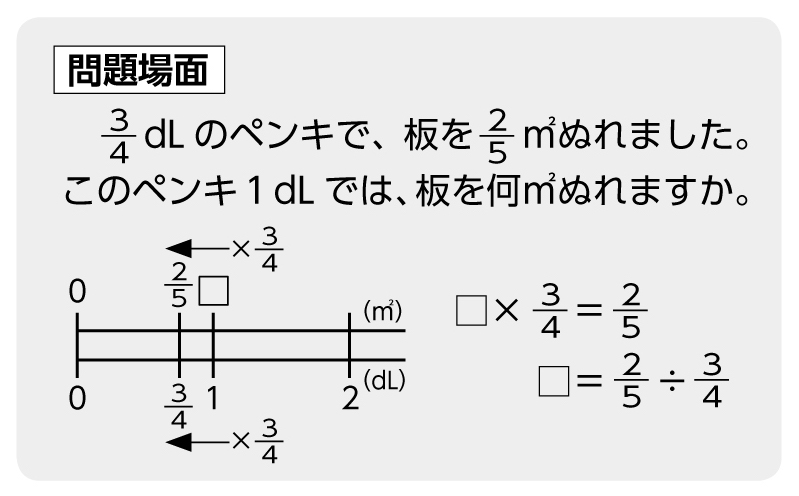



小6算数 分数のわり算 指導アイデア みんなの教育技術




小6算数 分数のかけ算 指導アイデア みんなの教育技術
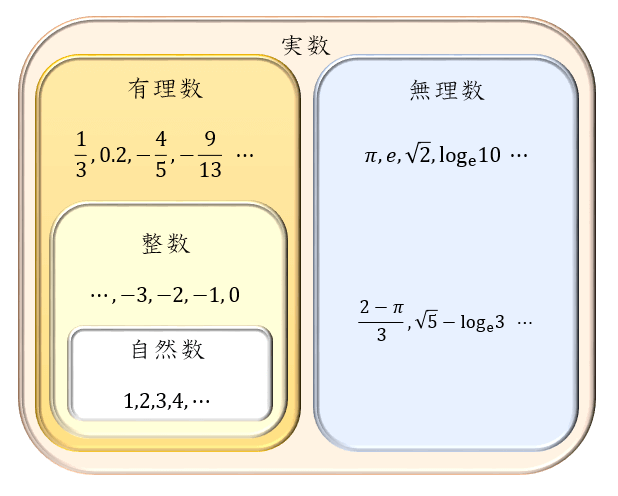



自然数 整数 有理数 無理数 実数とは何か 定義と具体例からその違いを解説 アタリマエ



分数は整数ですか 整った数字を分割している数字なので整数 Yahoo 知恵袋




分数 小数の変換方法 小学生に教えるための分かりやすい解説 数学fun




小数を分数にするやり方 大人の学び直し算数 計算のやり方解説 無料




分数の掛け算は なぜ分母同士 分子同士を書けるの 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服



Http Www Ogaki City Ed Jp Open Education Scholarship Math Plan 5nen 07 Pdf



6年算数 分数 整数 分数 整数 教え方のポイント



6年算数 分数 整数 分数 整数 教え方のポイント




中学受験講座 分数の計算 かけて整数になる計算 Youtube



3分の6って分数ですか 整数ですか 6 3は約分すると2 Yahoo 知恵袋
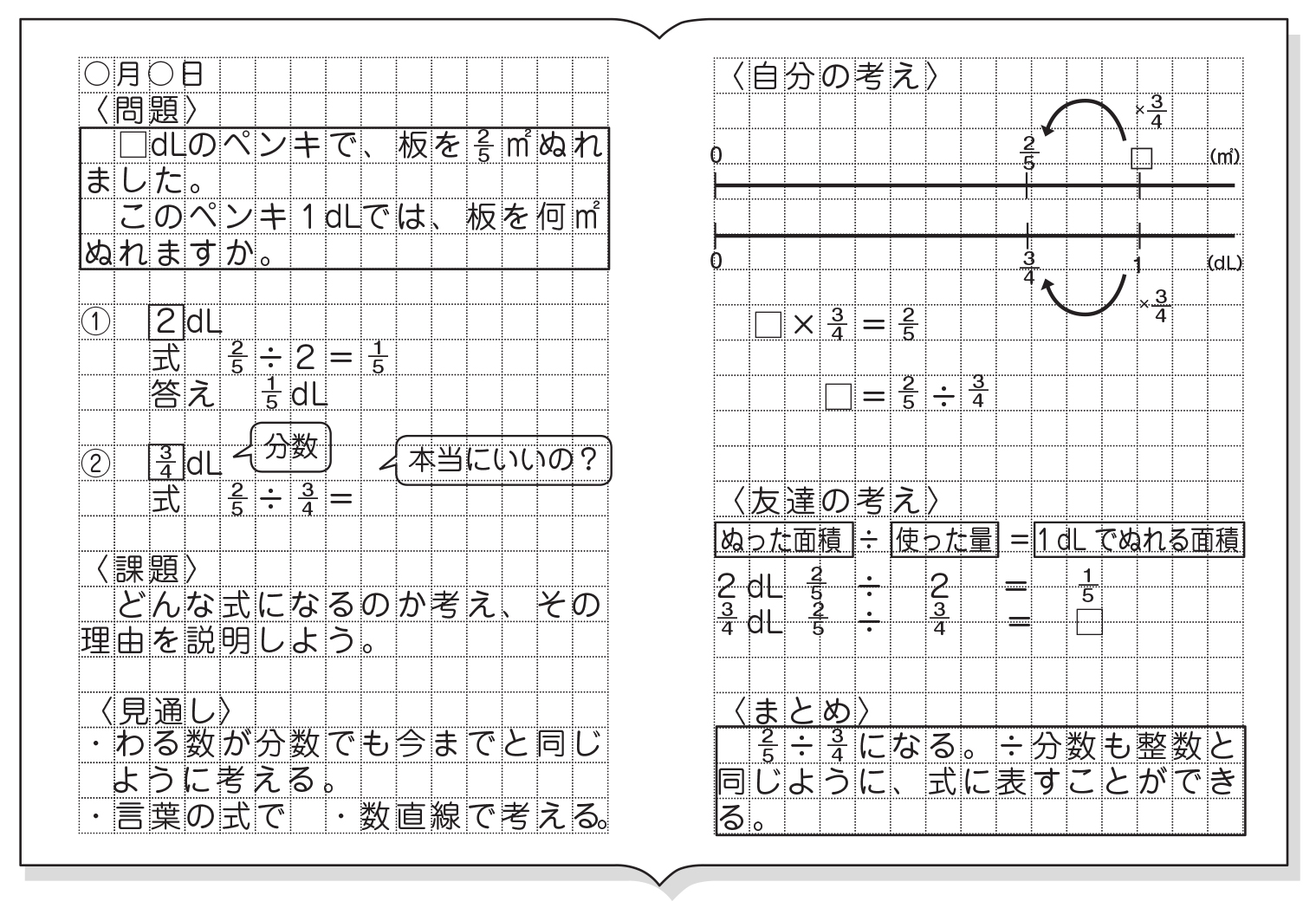



小6算数 分数のわり算 指導アイデア 1 みんなの教育技術




数学aの分数方程式の整数解についての質問です Clear



6年算数 分数 整数 分数 整数 教え方のポイント




帯分数の計算方法 足し算 引き算 掛け算 割り算 小学生への教え方のポイント 数学fun




6年算数 分数 整数 分数 整数 教え方のポイント



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料




数基礎 Com 分数と整数の割り算が分かる方法




分数と整数の足し算引き算が分からなくなってしまいました どなたか途中式や解説お願いい Clear
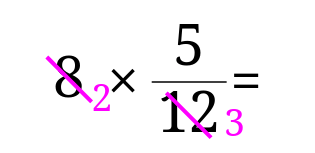



分数と整数の掛け算で約分があるときのやり方は どうやって説明する みけねこ小学校



3




分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun




整数とは 小学生でも簡単にわかる問題で 違いを覚えよう 中学や高校の数学の計算問題




中1の数学 正負の数や文字式 方程式は中学数学の基礎 家庭教師ジャニアス



3



小数と分数が混じった式の解き方 大人の学び直し算数 計算のやり方解説 無料
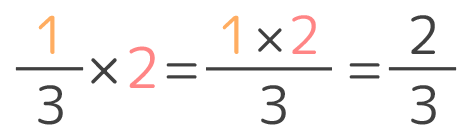



小学6年生 分数と分数のかけ算 のやり方は 分かりやすく教えます そうちゃ式 分かりやすい図解算数 別館



ドリルズ 小学5年生 算数 の無料学習プリント分数と整数のわり算




分数 整数の 黒板のイメージ かけ算の順序の昔話
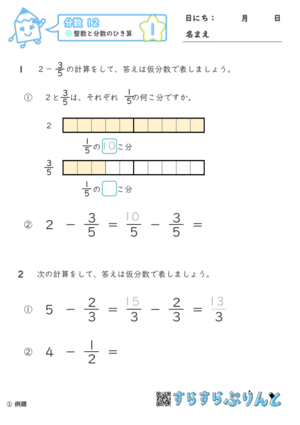



分数のひき算 整数ひく真分数 小学4年生算数 無料プリント



算数道場 1 数と計算8 分数と計算 その3 分数の種類
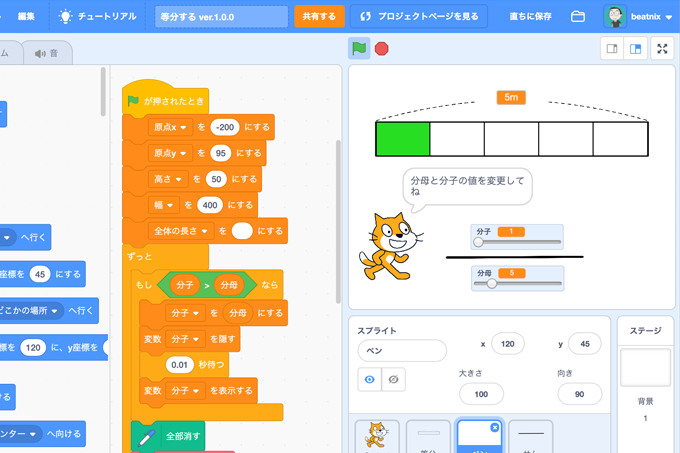



既存の教科でプログラミング授業 小学5年生 算数 分数と整数の関係 コドモとアプリ



今回は かけたら整数になる問題 分母が1になる分数は整数 オンライン授業動画です 約分 倍数 公倍数 公約数などの言葉があいまいになっていませんか 是非参考にして下さい O オンライン家庭教師授業動画 オンライン家庭教師 Zoom家庭教師 大阪 家庭教師 算数 関西




分数 小数は難しい 分数編 Z Square Z会




小学6年生の算数 分数 整数のかけ算 練習問題プリント ちびむすドリル 小学生



整数ってどんな数のことを言うんですか 小数とか 分数とかも入 Yahoo 知恵袋



4年算数 分数 1 わかる教え方のポンイト



分数のかけ算のやり方 小学校5年生 大人の学び直し算数 計算のやり方解説 無料
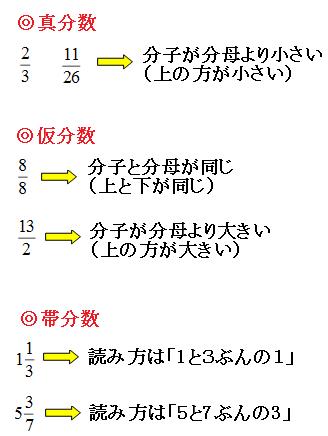



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利



整数とは 1分でわかる意味 自然数 少数との違い 負の数 0 分数との関係




東大問題にもチャレンジ 分数が整数になる条件 オモワカ整数 18 全21回 数学専門塾met Note
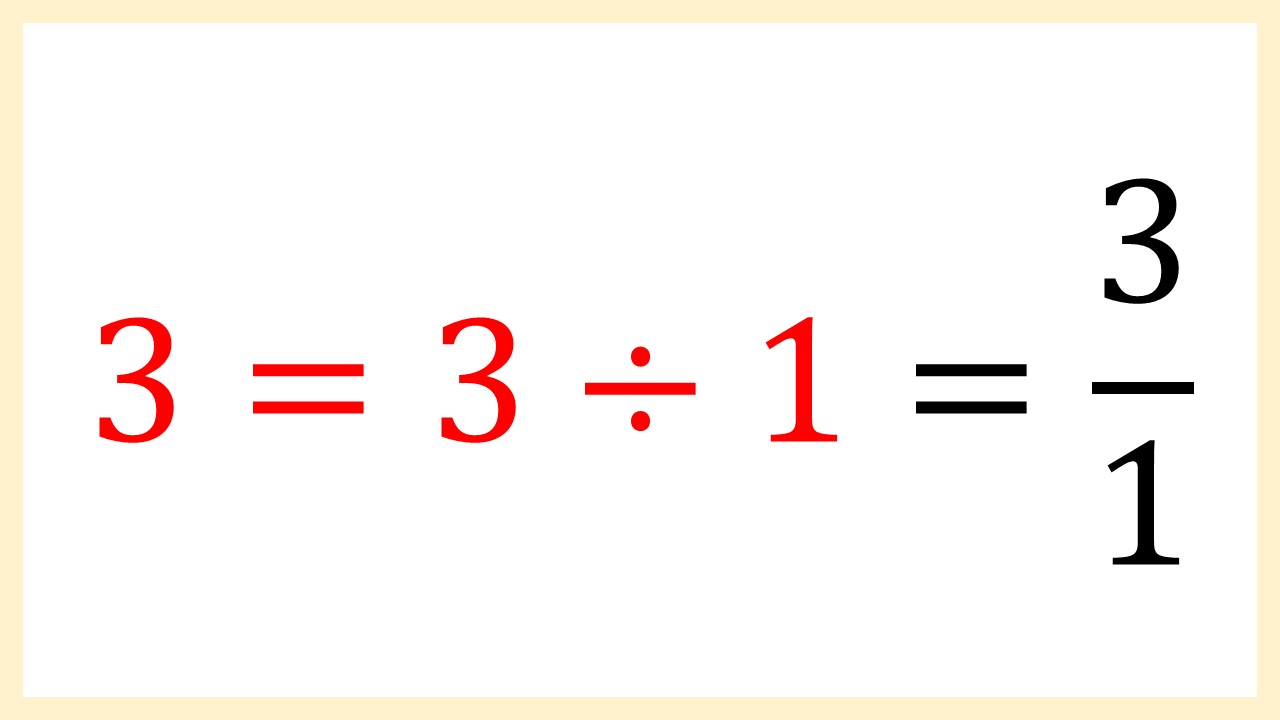



よくわかる 割り算を分数に直す方法 例題あり



Www Chofu Schools Jp Fujimidai Sho Documents 6sansua I Pdf



3年算数プリント 分数3



分数 タテ ヨコ 斜め 世界標準のスペック英語
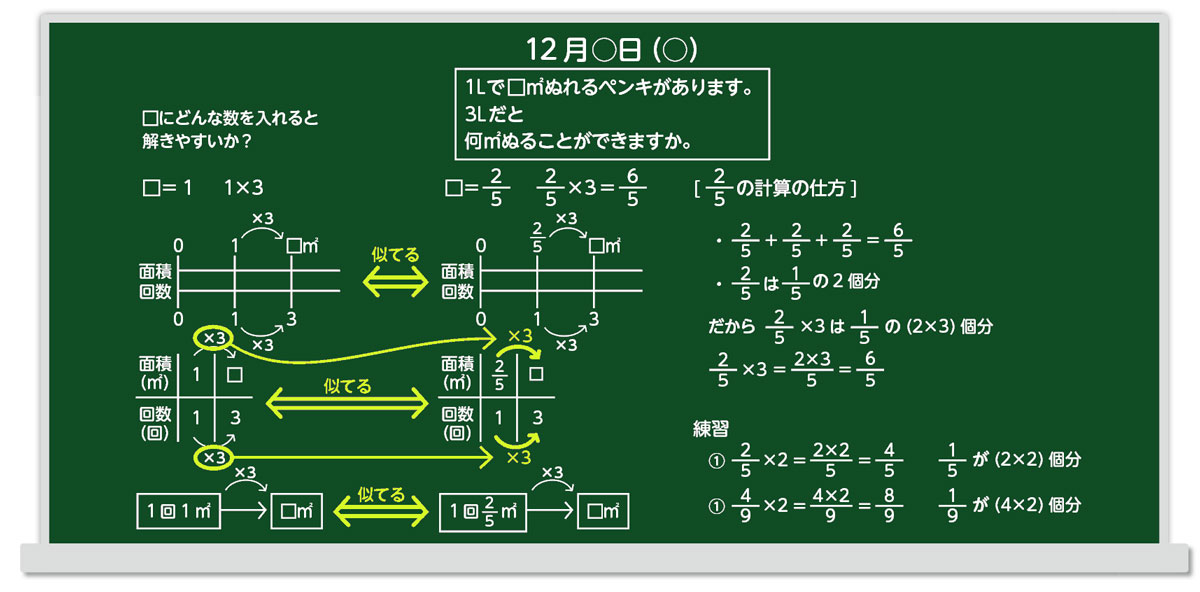



小学算数 構造的板書 の工夫とコツ 分数と整数 図形の角 みんなの教育技術
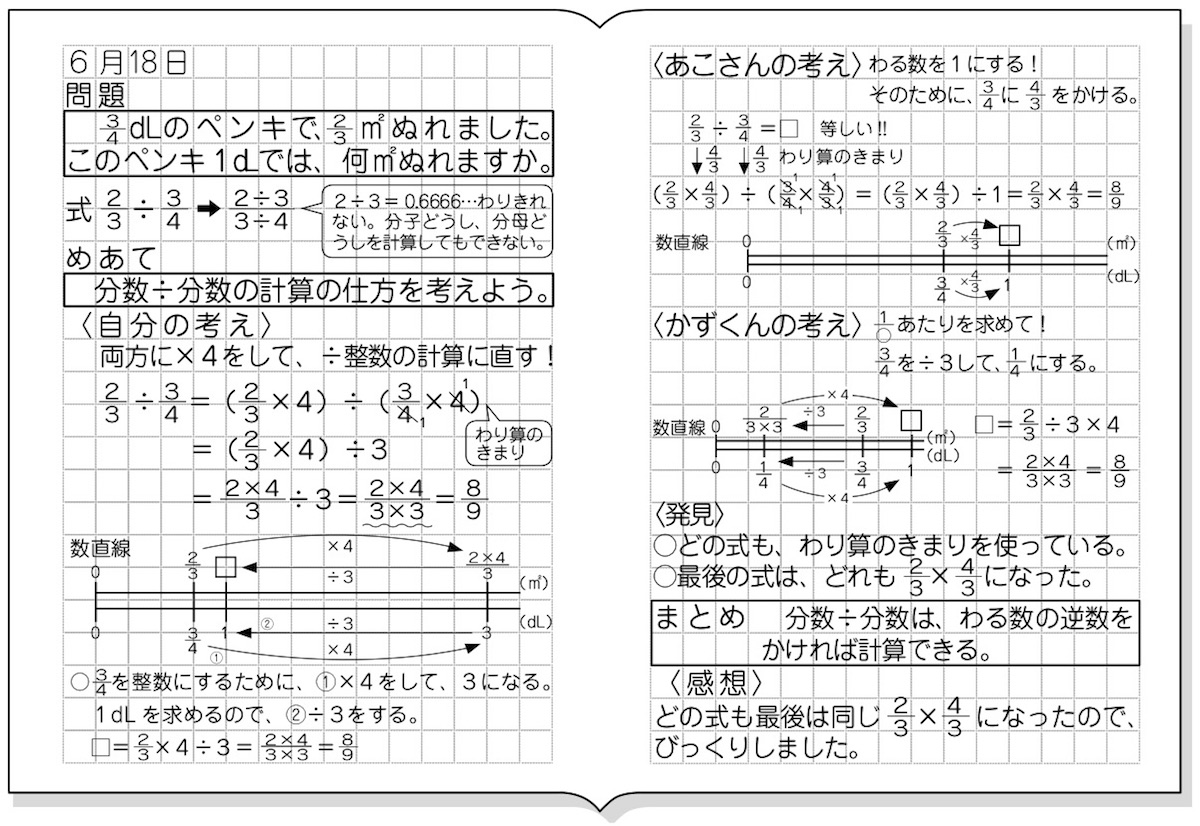



小6算数 分数のわり算 指導アイデア みんなの教育技術




110 Descubre Como Resolverlo En Qanda




仮分数を帯分数にする 問題練習 Youtube




平方根を分数の形にする方法を教えてください Clear



1



仮分数を整数か帯分数に直す 帯分数を仮分数に直すこれらの方法教え Yahoo 知恵袋


