42 両辺を100倍。 302 <↓平方根について,かんたんに解説しています。 みなさんは,「平方数」ということばを知っていますか? ではさっそく,かんたんな問題を出します。 問題 8の平方数はいくらでしょう。 ↓平方根の筆算のしかたを,解説しています。 例題として, という数の平方根を求めてみますルート・平方根の計算方法・仕方の3つのコツ ルート計算のコツはつぎの3つだ。 ルートを簡単にする 足し算・引き算はべつもの 分母は有理化しとく 練習問題をといてみよう。 つぎのルートの計算をしてください。 √8 √2分の5 – √3 ×

三平方の定理の証明と使い方
平方根の定理とは
平方根の定理とは-16の平方根は、±4 25の平方根は、±5 とすぐ答えることができます。 「平方根は、いつも2つある」 ことを、 忘れないでくださいね! 「2乗になる数」がない?? では、ここから先が「ルート」の話です。 いきなり質問から。 「3の平方根は?平方根 平方根(1) 問題一括 (8,085Kb) 解答一括 (9,324Kb) 平方根(2) 平方根の大小 有理数と無理数 平方根の乗法 平方根の除法 平方根の性質(1) 平方根の性質(2) 平方根の近似値 根号を含む計算 有理化 平方根の加法・減法(1) 平方根の加法・減法(2) 平方根の



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
平方根の定義 a a を実数とします. 2 2 乗すると a a になる数のことを a a の 平方根 と言います.言い換えると, a a の平方根とは, 2 2 次方程式 x2 = a x 2 = a の解のことです. 正の実数 a a の平方根は必ず 2 2 つあり,それらは絶対値が等しく,符号が異なり1.単元名 「平方根」 2.単元について 私たちの生活の中には、黄金比や白銀比などのように、有理数だけでは表せない無理数が存在している。 また、無理数は有理数を2辺とする直角三角形の斜辺に表れており、土地の測量の場面で活用されている。 しかも、それらは、有史前より、感覚的には は ×
10 上式は次式と同等。 13 59 <のようになります。 stdhypotを利用した場合、以下のように書けます。 z = std hypot (x,y);Created Date AM
平方根および立方根を取得して画面に表示しました。 Java で数値の平方根または立方根を取得する方法について解説しました。 ( Written by Tatsuo Ikura ) 関連記事 (一部広告含む) Profile 著者 / TATSUO IKURA 初心者~中級者の方を対象としたプログラミング方法や開発環境の構築の解説を行う2 第12 章 平方剰余 証明 k が偶数ならば明らかにa は平方剰余である.逆にa が平方剰余であると仮定し てk が偶数であることを示そう.a が平方剰余ならば,x2 ≡ a (mod p) をみたすx ∈ Z が存在する.g が原始根であることよりx ≡ gl (mod p) となる整数l がとれて, g2l ≡ x2 ≡ a ≡ gk (mod p)4の平方根というのは、2乗して4になる数のことだから $$\Large{2^2=4}$$ $$\Large{(2)^2=4}$$ このように\(2, 2\)が見つかります。 よって、 4の平方根は\(2\)と\(2\) だということになります。 基本的に平方根は、このように+と-の数がセットで出てきます。 なので、これらをまとめて




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




中3数学 図でよくわかる三平方の定理 ピタゴラスの定理 の証明と計算問題 Irohabook
平方根計算機 オンラインの平方根計算機を使用して、入力した数値の平方根を見つけます。 平方根 数学では、数値xの平方根は、r 2 = xとなるような数値rです。 例えば、 1 5 2 = 25であるため、25の平方根は5です。 3 2の平方根はおよそです。 3 Piの平方根(π)は約です平方根とは 2 乗すると a になる数のことを a の平方根といいます。つまり、式 x 2 = a の x に当てはまる数が a の平方根です。1 つの正の数に対して、その平方根は正と負の 2 つあります。 平方根は、二乗根や自乗根と言われることもあります。 平方根の計算中学3年生 数学 計算たしかめミックス 練習問題「式の展開と因数分解」「平方根」「2次方程式」 中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード・印刷 中学3年生 数学 平方根の加法・減法 問題プリント 無料




三平方の定理 を使わずに解いてみよう 大阪星光学院 数学カフェjr




必見 絶対知りたい三平方の定理の証明方法3選 見やすい図で即わかる 高校生向け受験応援メディア 受験のミカタ
平方根 へいほうこん square root 実数 a に対して,x 2 =a を満たす実数 x を a の平方根と呼ぶ。 a が正数のとき a の平方根は正数であるものと負数であるものの二つが存在し,このうち正の方を√a で表す。 0の平方根は 0である。たとえば,√2=,√3=であり,これらはSqrt()は、平方根を求める関数です。sqrt()を利用した場合、 z = sqrt (x * x, y * y);定理(Abel) n 5の場合,一般にはn次方程式の根を方程式の係数から加減乗除とべき根 をとる操作のみを用いて求めることはできない. この定理は16年の論文でAbelにより証明されました. 17 根の個数 定理13を用いると,複素数係数のn次多項式 f(x) = xn a n 1x n




國三 Junior High数学的 数学 三平方の定理 筆記 Clear



1
平方根とは何かということを理解するにおいて、必須の概念が「2乗」です。 2乗とはある数を2回かけること。 たとえば2の2乗は4、3の2乗は9です。 そして、平方根とは「2乗」の逆の概ってかんじで平方根をみつけてみようw あと、じつはね。 平方根にはプラスとマイナスの2パターンある んだ。 だから、25の平方根は5のほかにも、5 があるよ。 なぜなら、5を2回かけても25になるからね。 こんな感じで、 ある数の平方根は「」と「」の在數學中,一個數 的平方根 指的是滿足 = 的數,即平方結果等於 的數。 例如,4和4都是16的平方根,因为 = = 。 任意非負實數 都有唯一的非負平方根,称为算术平方根或主平方根(英語: principal square root ),記為 ,其中的符号√称作根号。 例如,9的算术平方根为3,记作 = ,因为 = = 并且3非



ピタゴラスの定理 Wikipedia




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ
平方根は「 ボールを投げたときの放物線運動 (二次方程式の解の公式)」や「 株価の変動リスク の評価(標準偏差)」など、色んな分野の計算法が見えてくるので、理解できる世界がグッと広がってくる単元です。 ぼく自身、複雑にみえていた色んな数式を自分でも解けるようになって平方根を計算することは、x 2 =aとなるxの値を求めることになります。 また、中学校では a が0以上の数である場合のみを勉強します。 なぜなら、2乗して負の数になる数は存在しないからです。 ※ 高等学校では、2乗して負になる数も学習します(虚数)(ak)l≡1 ⇔ akl≡1 ⇔ klは素数eの存在定理と平方剰余の相互法則倍数 であるから,フェルマーの小定理により0<l<e の存在定理と平方剰余の相互法則と平方剰余の相互法則きに素であるとする。(ak)l≡1 と平方剰余の相互法則な整数るl が成り立つ。存在しな整数いための存在定理と平方剰余の相互



中学数学 三平方の定理




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく
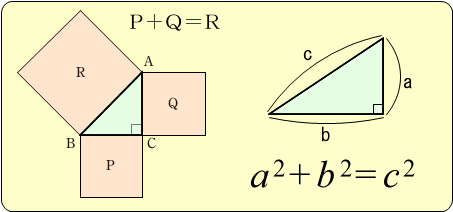
二乗和の平方根は、三平方の定理と関係します。下式をみてください。 c=a 2 b 2 d=√c 両辺を2乗すると、 d 2 =a 2 b 2 です。dを斜辺、a、bを底辺、高さと考えれば、三平方の定理(ピタゴラスの定理)となります。三平方の定理の証明などは下記が参考になります。 ピタゴラスの定理とは?1分中3 学習単元一覧 式の展開 因数分解 平方根 2次方程式 2乗に比例する関数 図形の相似 三平方の定理 円の性質 標本調査 式の展開式の展開の基礎乗法公式1乗法公式2平方根(ルート) 平方根の利用正方形の対角線、丸太、自然数を求める解き方は? いろんな利用問題を解説! kaztaro 中学数学・理科の学習まとめサイト! 平方根(ルート) ★有理化の仕方★やり方をまとめておくよ! 中学生 kaztaro




大工の算数 ピタゴラスの定理 小屋をつくった16年暮らした




中学数学 三平方の定理の証明 中学数学の無料オンライン学習サイトchu Su
特に 実数 の範囲では、正の実数の平方根は、互いに 反数 である2個の実数となる。 幾何学 的には、正の実数の平方根の内、正の方は、与えられた 正方形 の 面積 に対するその一辺の長さのことである。定理・公式・証明高校数学定理・公式 – 数学Ⅰ – 平方根の性質・2重根号 Twitter Facebook はてブ Pocket LINE コピーが成り立ちます.(これを三平方の定理 根号の中を1つの数字に直してからルート(平方根のうちの正の方)を考えること は ×



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ
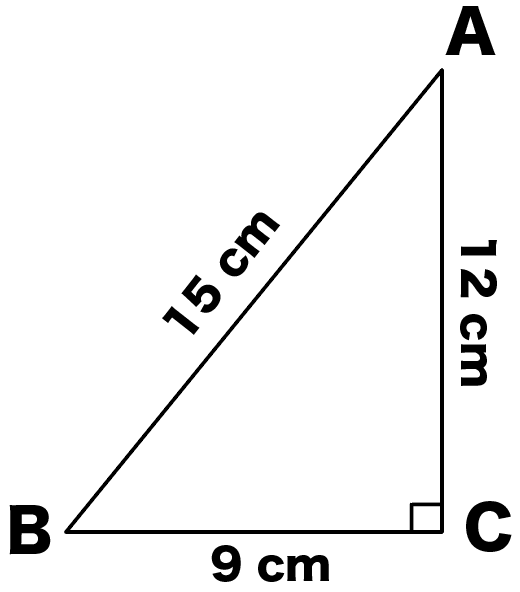
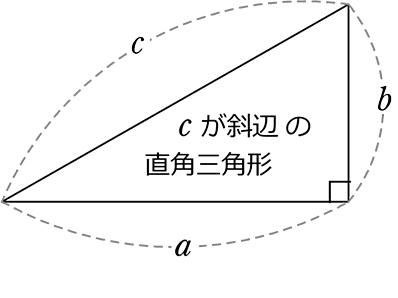
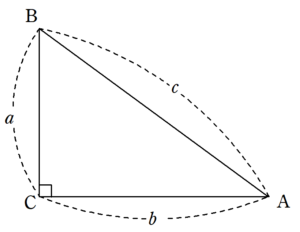
三平方の定理 (さんへいほうのていり)、 勾股弦の定理 (こうこげんのていり)とも呼ばれる。 ピタゴラスの定理によって、直角三角形をなす3辺の内、2辺の長さを知ることができれば、残りの1辺の長さを知ることができる。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru正整数 の平方根の整数部 = 351 正整数 の平方根の整数部 = 3513 ok 改良 1234の平方根を求める。 1234を2桁ずつに分ける。 ①12の平方根を求める。 0 <




コラム ピタゴラスの定理 江戸の数学




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座
ルートとは?平方根の求め方を解説!分数や小数の場合はどうやる? 平方根、ルートの値を語呂合わせ!覚え方まとめ←今回の記事 a√bの形に変形するやり方とは? 平方根の大小関係を不等号で表す問題を解説! 根号を含む式の値の求め方とは?は 根号の中で2乗になっている数は外に出ると1つになる.1つしかないものは出られない. 根号の中に3個あるものは2個と1個に分ける 《問題2》 次のは偶奇の等しい整数であるので, α β \alpha\beta αβ もまた O O O の要素である (3) N ( α) = a 1 a 2 5 2 ⋅ a 1 − a 2 5 2 = a 1 2 − 5 a 2 2 4 N (\alpha ) = \frac {a_1a_2\sqrt 5} {2}\cdot\frac {a_1a_2\sqrt 5} {2} = \frac {a_1 {}^25a_2 {}^2} {4} N (α) = 2a1




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4




数学 中3 61 三平方の定理 基本編 Youtube
平方根応用 (図形) 図の ABCはAB=AC,∠BAC=90°の直角二等辺三角形である。 頂点Aから辺BCに垂線をおろしその交点をPとする。 AP=2cm, BC=4cmのとき次の問いに答えよ。 ABCの面積を求めよ。 辺ABの長さを求めよ。平方根とは 平方根とは2乗の逆のこと 「5の2乗は25、また、 (−5)の2乗も25である。 」 そのため25の平方根は5と−5である。 5と5のことをあわせて±5と表記することもある。 例) 25の平方根は±5 平方根とは2乗の逆のことなので、 2乗したときにAになる数算术平方根及勾股定理 练习题 一:填空选择题 1下列图形中,面积最大的是( (a)边长为 3 的正方形 (b)边长为 2、高为 1 的平行四边形 (c)对角线长分别为 4 和 1 的菱形




三平方の定理 ピタゴラスの定理 の計算問題 の3つの解き方 Qikeru 学びを楽しくわかりやすく




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
102 ニュートン法から得られる平方根,立方根,4乗根の連分数表示 定理3 連分数表示の漸化式 は,平方根 ±√a を求める式である. (2.1.7)の分母に(1.2)の右辺の漸化式があることに注意せよ. となる.x0=1 ここで とおくと となり, √2 =1.可逆行列 a に対して、ユニタリ行列 u および正定値行列 p が一意に存在して a = up と書ける。 これを a の極分解と呼ぶ。 この正定値行列 p は正定値行列 a*a の主平方根であり、 u は u = ap −1 で求まる。 a が可逆でないときでも、適当な方法で p が定まれば(それは一意であり)極分解2平方定理この定理はフェルマーの2平方定理とも呼ばれることがあり,証明はオイラーによってはじめてなされたとされています.定理.奇素数(奇数かつ素数,すなわち 3 以上の素数) \(p\) が 4 で割ると 1 余るとき,\(p\) は 2



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス



三平方 平方根




三平方の定理の証明と使い方



かみのドリル 三平方の定理




三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト



最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中3数学 三平方の定理とは 練習編 映像授業のtry It トライイット



三平方の定理の証明 中学生向けの方法を6つ紹介 ヒデオの情報管理部屋all Rights Reserved



1




最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



ビッグバン宇宙の菅数論 三平方根の定理で考える円積問題 発想力教育研究所 素数誕生のメカニズム



三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に



三平方の定理の証明 アン コンディットの証明 Fukusukeの数学めも




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



数の不思議 奇数の和でできるピタゴラス数 Note Board




最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



直角二等辺三角形と三平方の定理の関係は 3分でわかる計算 公式 辺の比 例題




三平方の定理の証明と使い方
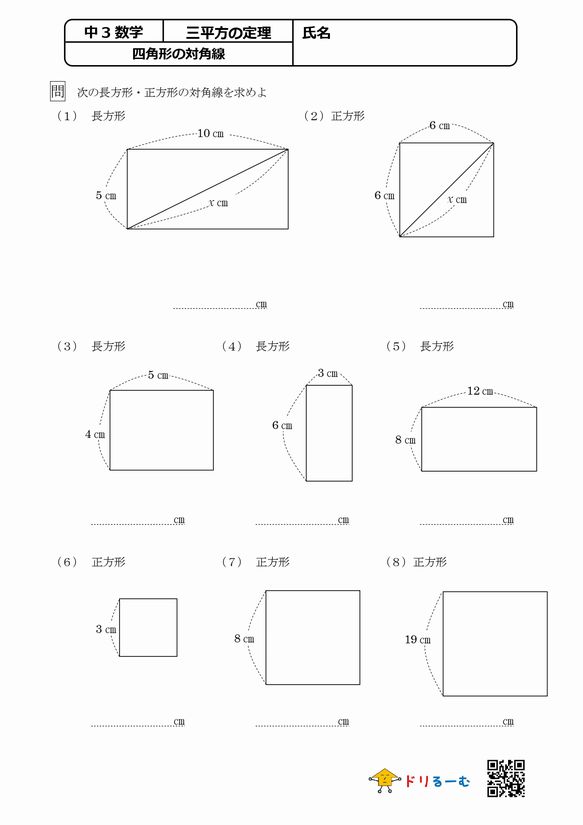



三平方の定理 四角形の対角線 ドリるーむ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理で辺を求める Youtube




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理の証明と使い方
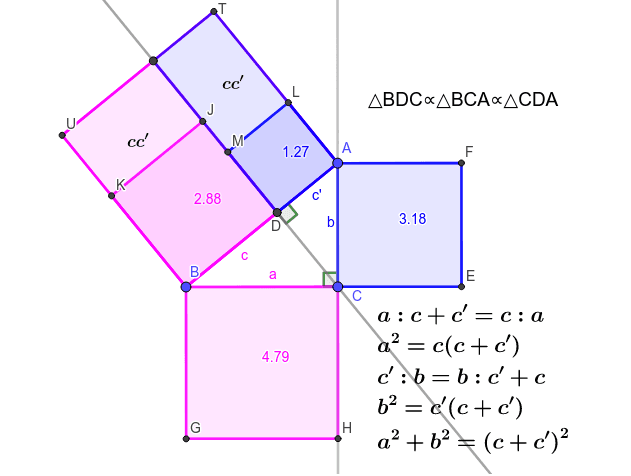



ピタゴラスの定理の拡張 その1 Geogebra




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



1



1




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導



三平方の定理
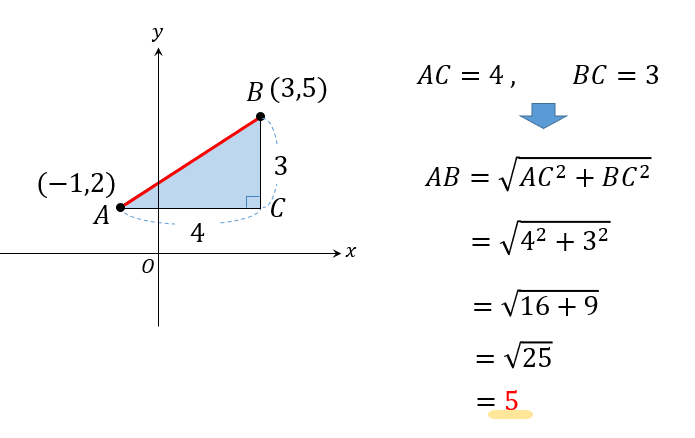



中学数学 二点間の距離の求め方をイチから解説 数スタ




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube




70以上 三 平方 の 定理 証明 中学生 ニスヌーピー 壁紙
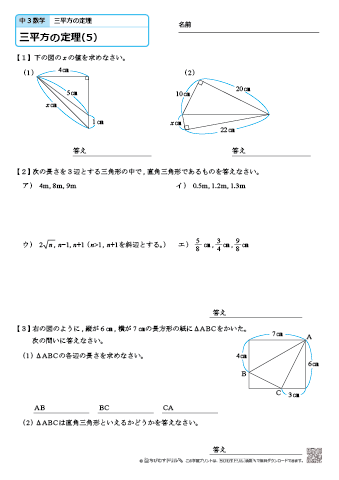



中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社
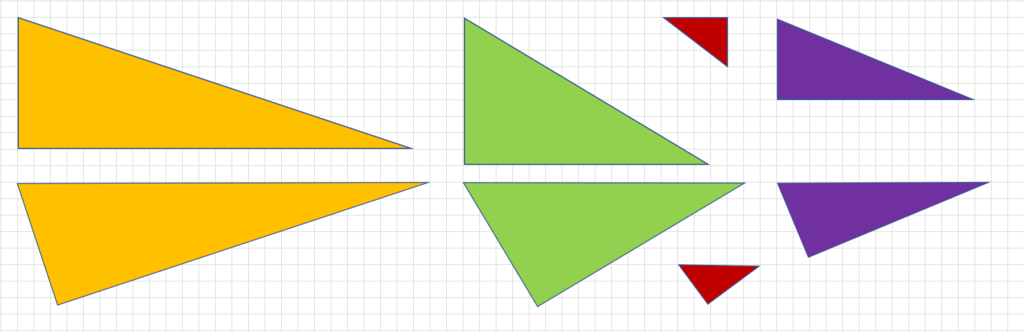



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog



ピタゴラスの定理とその拡張




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




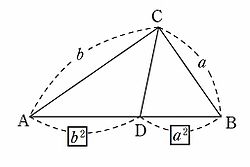
ピタゴラスの定理 Wikipedia
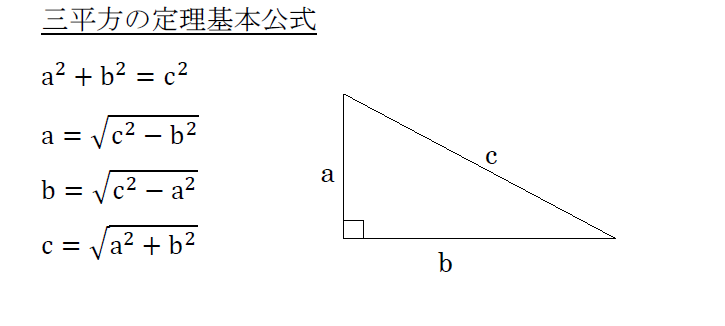



受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学




三平方の定理と二等辺三角形 Youtube




最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ
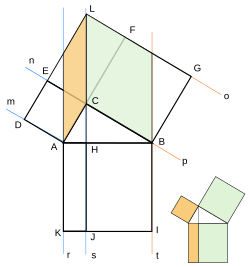



ピタゴラスの定理 Wikipedia




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理の4通りの美しい証明 高校数学の美しい物語




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
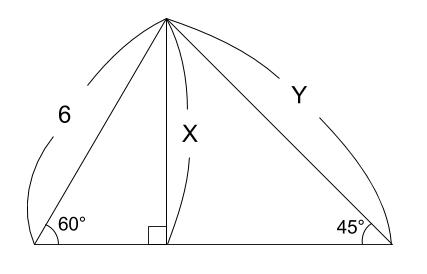



中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理 覚えておきたい基本公式を解説 数スタ
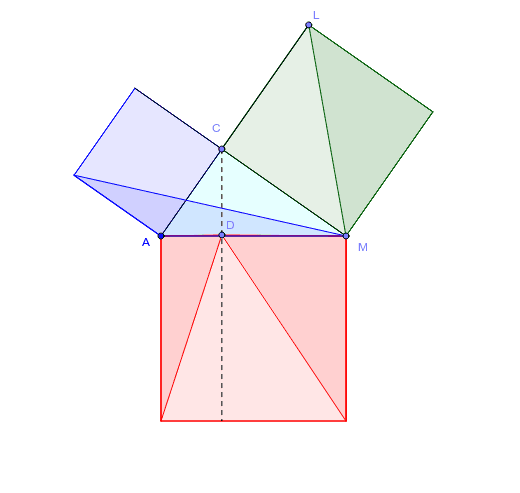



ピタゴラスの定理から余弦定理へ Geogebra




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
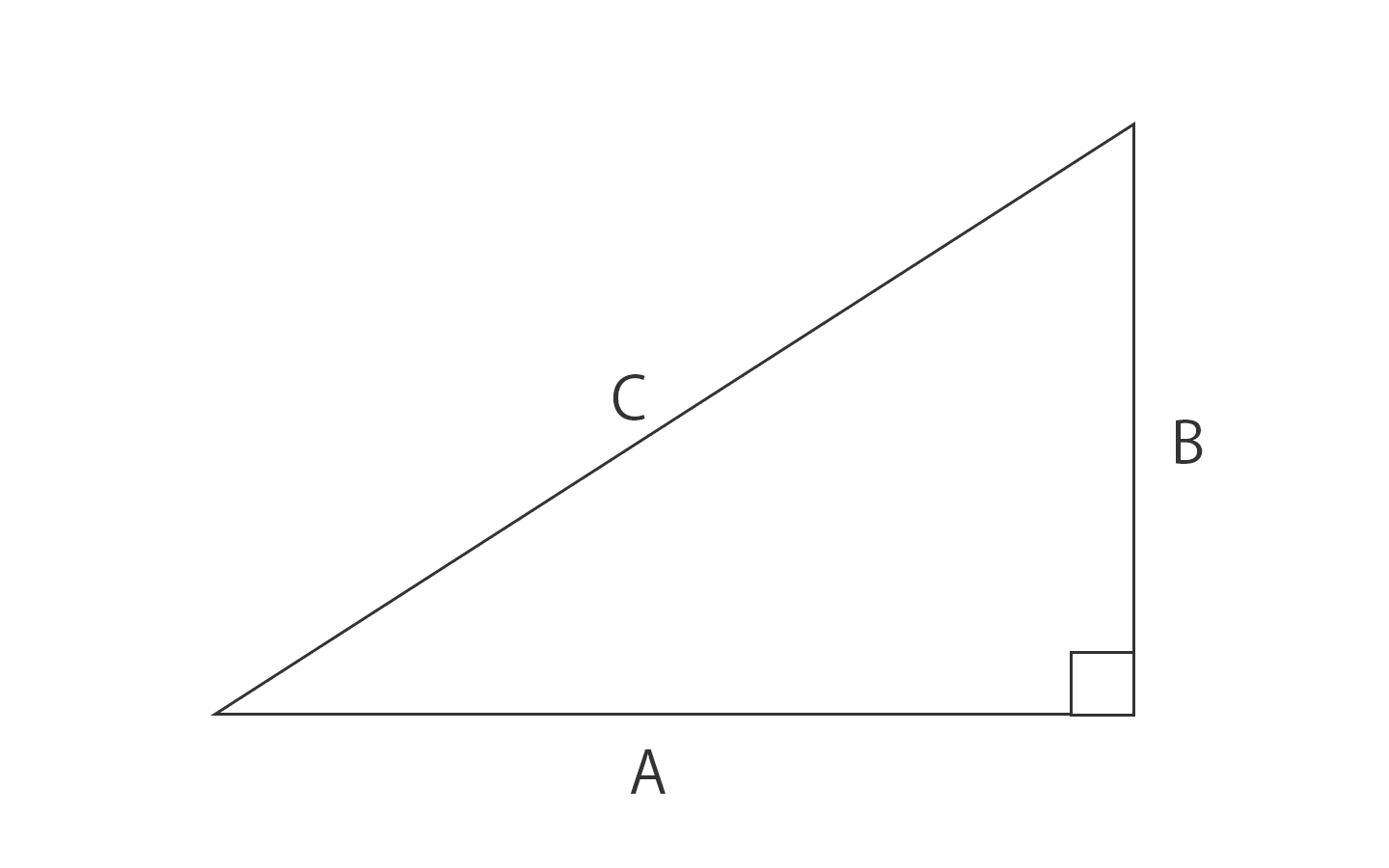



Python 三平方の定理 Unpyside




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




ピタゴラスの定理 Wikipedia



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド
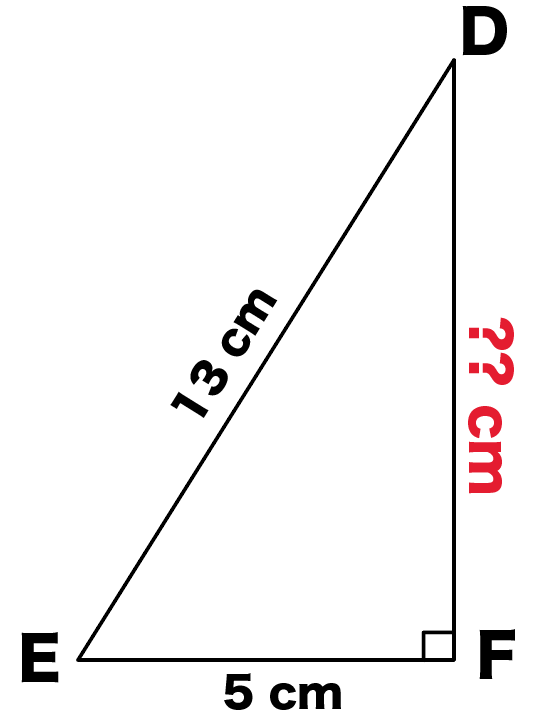



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく




ピタゴラスの定理 Wikipedia




中3数学 三平方の定理とは 例題編 映像授業のtry It トライイット




中 3 数学 三 平方 の 定理 シモネタ
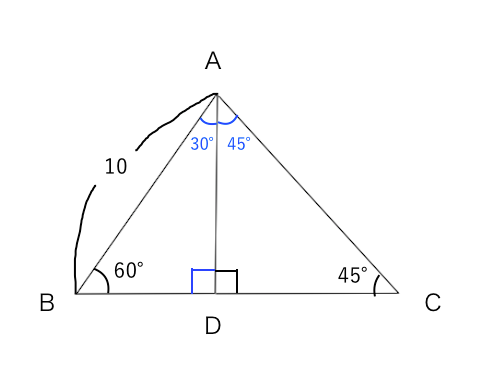



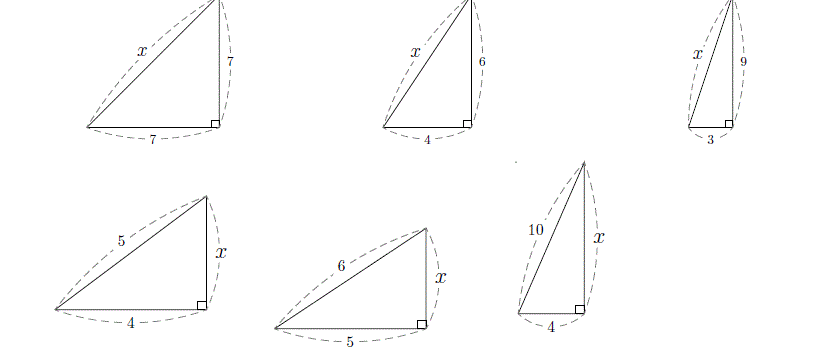
三平方の定理 練習問題 苦手な数学を簡単に



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
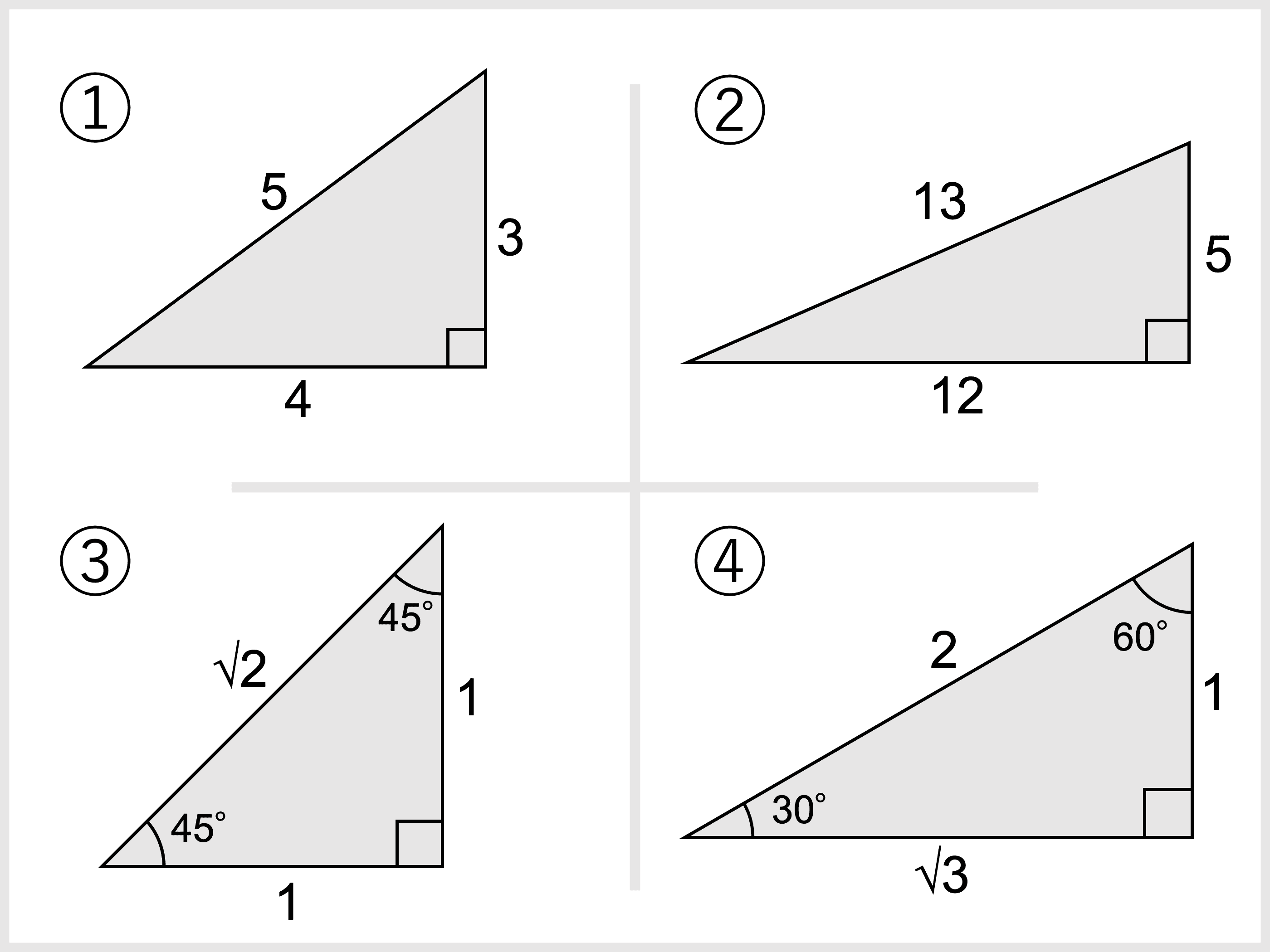



最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学
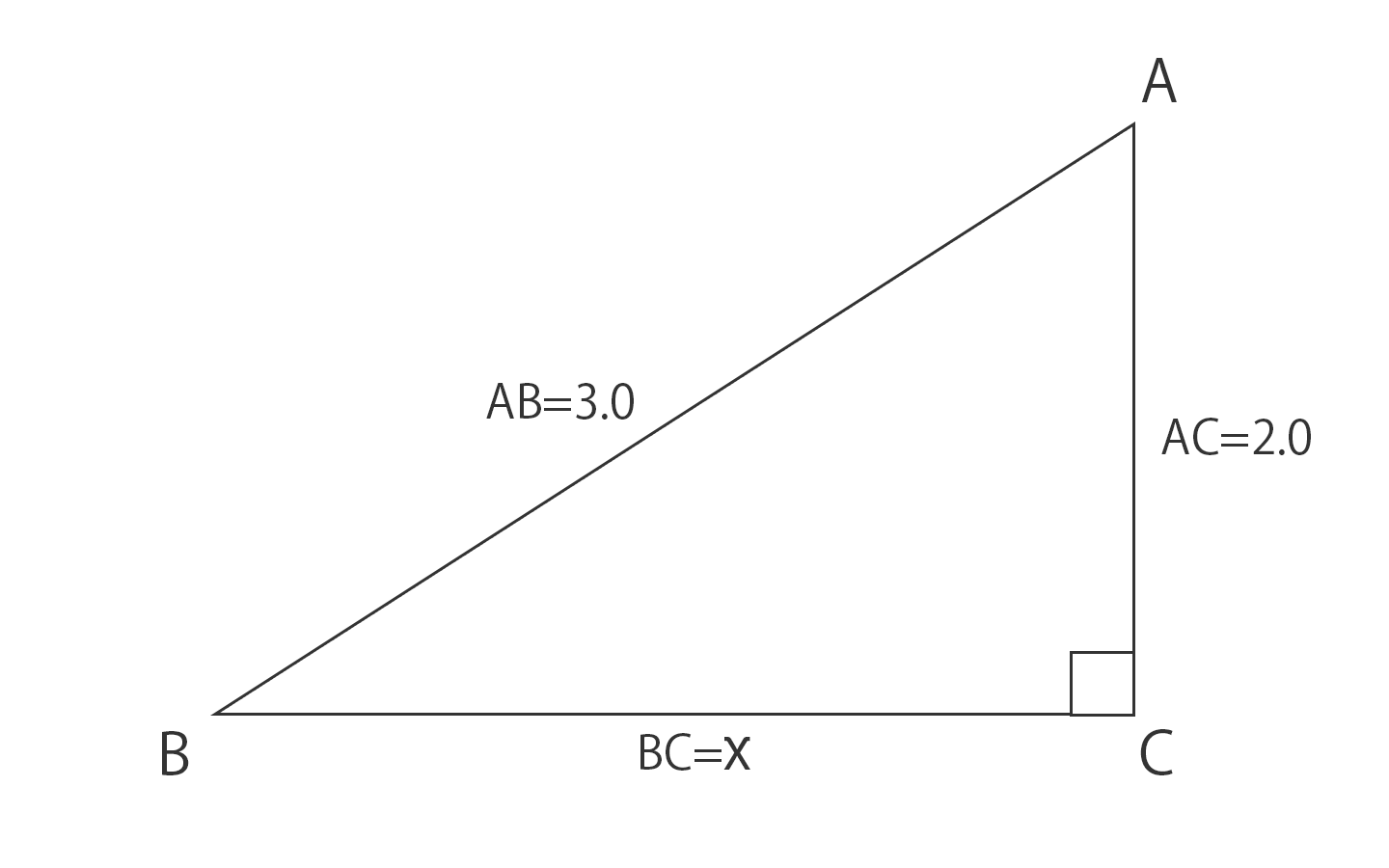



Python 三平方の定理 Unpyside



日曜大工で使う数式




三平方の定理を使って面積を求める方法は 問題を使って解説するよ 中学数学 理科の学習まとめサイト



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ


